这是一个创建于 1402 天前的主题,其中的信息可能已经有所发展或是发生改变。
我看过至少两个老师讲的拉格朗日乘数法。都大致基于以下思路。讲授一般是通过例题给出,例如:求 xy=3 到原点距离最近的点的坐标。于是该问题转化为
距离函数 f(x,y)=x^2+y^2 和 约束函数 g(x,y)=xy=3 。求距离函数 f 在满足约束函数 g 的约束条件的前提下求 f 最小值的问题!
该问题的几何图形表现为 f(x,y) 与 g(x,y)相切于一点,且 f 的最小值出现在 f 与 g 相切的哪一点
共切点则共切线,共切线则法线平行,于是后面根据法线平行,引出了拉格朗日系数。后面不再赘述。
我的困惑在于,上面的例子过于理想化(为了教学的形象化,找理想化的例子没问题)。但是这种特殊例子得出的结论是否具有普遍性呢?
假设我们换一种表述。不是求 g(x,y) 距离原点最近的那一点的坐标。我们直接给一道题 求 f(x,y)的极值,同时 x,y 满足 g(x,y)=C,C 是常数。g 是约束函数。f 可以是任意函数,唯独不是 x^2+y^2 的形式。那么拉格朗日乘数法还适用么?
例题的逻辑思路是:
1 、求 g(x,y)上到原点距离最短的点的问题 ,转化为求 f(x,y)在满足 g(x,y)约束的情况下求 f(x,y)极值的问题。
2 、求 f(x,y)极值的问题,转化为 f(x,y)与 g(x,y)切点的问题。前提是 f(x,y)是一个距离函数!!!!
3 、切点问题转化为共切线。
4 、共切线问题转化为法线平行的问题!
5 、法线平行引出拉格朗日乘数法。
但是一旦 f(x,y),不再是一个距离函数,那么 f(x,y)极值点还一定是 f(x,y)和 g(x,y)的公共切线的交点么?如果不是,那么后面的 3-5 步是不是都不成立了?那么拉格朗日乘数法是不是有使用限制呢?
如果我的担忧是多余的。是否有什么几何的讲授方法可以打消这种对普遍性的顾虑呢?
距离函数 f(x,y)=x^2+y^2 和 约束函数 g(x,y)=xy=3 。求距离函数 f 在满足约束函数 g 的约束条件的前提下求 f 最小值的问题!
该问题的几何图形表现为 f(x,y) 与 g(x,y)相切于一点,且 f 的最小值出现在 f 与 g 相切的哪一点
共切点则共切线,共切线则法线平行,于是后面根据法线平行,引出了拉格朗日系数。后面不再赘述。
我的困惑在于,上面的例子过于理想化(为了教学的形象化,找理想化的例子没问题)。但是这种特殊例子得出的结论是否具有普遍性呢?
假设我们换一种表述。不是求 g(x,y) 距离原点最近的那一点的坐标。我们直接给一道题 求 f(x,y)的极值,同时 x,y 满足 g(x,y)=C,C 是常数。g 是约束函数。f 可以是任意函数,唯独不是 x^2+y^2 的形式。那么拉格朗日乘数法还适用么?
例题的逻辑思路是:
1 、求 g(x,y)上到原点距离最短的点的问题 ,转化为求 f(x,y)在满足 g(x,y)约束的情况下求 f(x,y)极值的问题。
2 、求 f(x,y)极值的问题,转化为 f(x,y)与 g(x,y)切点的问题。前提是 f(x,y)是一个距离函数!!!!
3 、切点问题转化为共切线。
4 、共切线问题转化为法线平行的问题!
5 、法线平行引出拉格朗日乘数法。
但是一旦 f(x,y),不再是一个距离函数,那么 f(x,y)极值点还一定是 f(x,y)和 g(x,y)的公共切线的交点么?如果不是,那么后面的 3-5 步是不是都不成立了?那么拉格朗日乘数法是不是有使用限制呢?
如果我的担忧是多余的。是否有什么几何的讲授方法可以打消这种对普遍性的顾虑呢?
1
gaint97 2021-03-18 21:24:13 +08:00 via iPhone
忘了,啥是距离函数?函数不都有极值吗
|
2
huzhikuizainali OP @gaint97 可以复习一下就可以想起来了
|
3
RingoTC 2021-03-18 23:37:13 +08:00
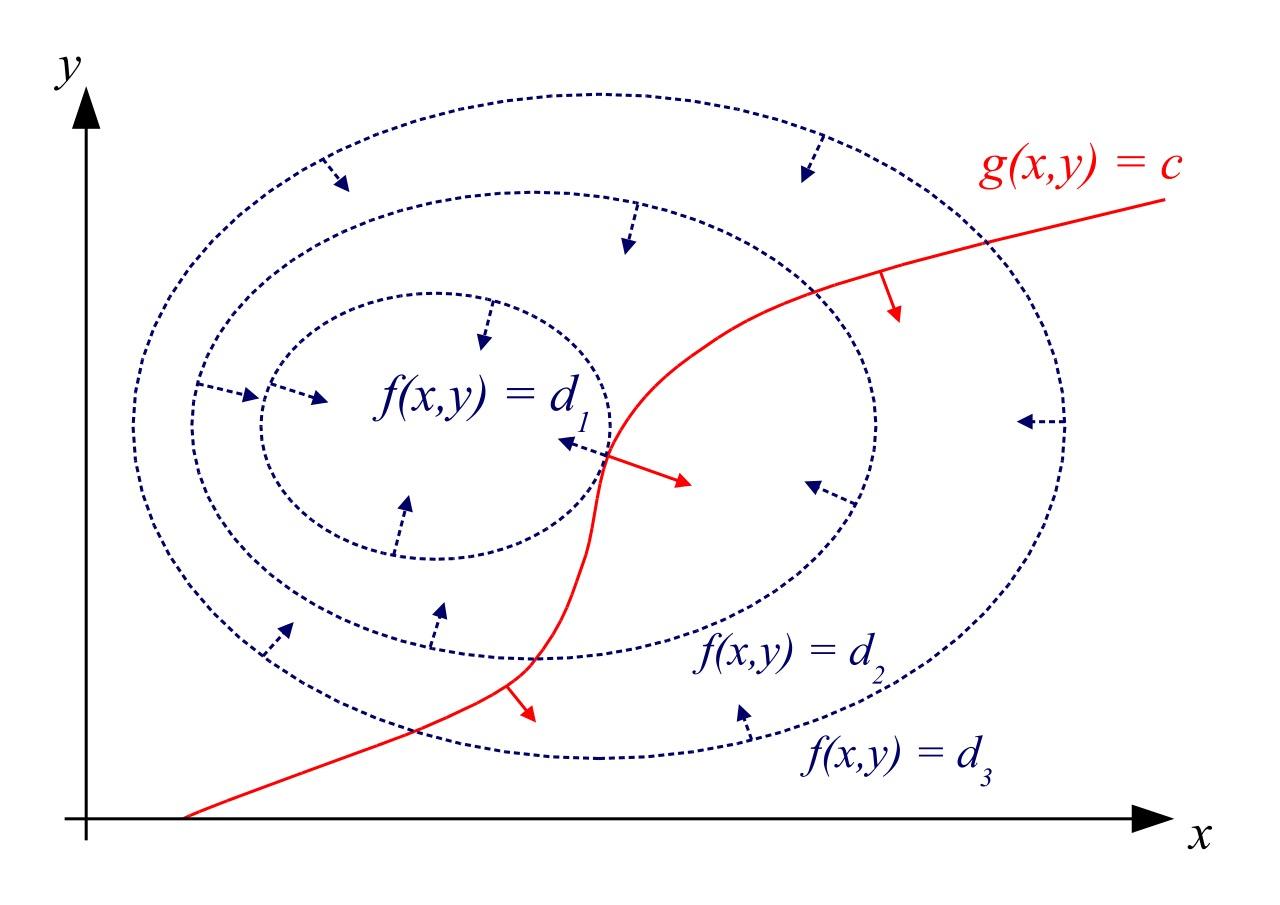
考虑上述例子,红色线为约束 g(x,y)=c,蓝色为 f(x,y)的等高线。 那么,在约束上,一定是与等高线相切处取得条件极值。 如果当前不在切点,那么一定有比当前值更小 /大的值。 |
4
hsfzxjy 2021-03-19 01:19:34 +08:00 via Android
你所听到过的拉乘的(几何)解释只是为了让你能比较形象地明白一些特殊情况,但拉乘适用于一般的约束极值问题,优化目标可以是很普遍的函数。
|
5
dji38838c 2021-03-19 01:48:12 +08:00
这么讲吧:
假如在约束函数上,存在:那么一个极值点(x0, y0),而且它的 f, g 的法线方向不一致。 那么,我就可以把 f 的梯度向量, 分解成沿着 g 的,和垂直于 g 的,然后向着沿着 g 的方向走一点点,就可以取得更小值了, 这就和“(x0, y0)是极值点的假设矛盾了” |
6
geelaw 2021-03-19 03:34:34 +08:00
用隐函数定理理解也很简单,考虑 f(x, y) 在 g(x, y) = 0 约束下的极值。
假设极值点邻域内 g(x, y) = 0 可以显化为 y = y(x),则在这一点 h(x) = f(x, y(x)) 具有极值,因此 h'(x) = 0 即 f_x(x, y(x)) + f_y(x, y(x)) y'(x) = 0. 注意 n = (1, y'(x)) 是隐函数在该点处切线的法向量,隐函数求导定理表明该向量和 grad g = (g_x(x, y(x)), g_y(x, y(x))) 正交,而 grad f = (f_x(x, y(x)), f_y(x, y(x)))。 也就是说 n 和 grad g 、grad f 都正交,因此 grad g 和 grad f 线性相关。 考虑乘子函数 F(x, y, k) = f(x, y) + kg(x, y),可以看出 F 仅当 g(x, y) = 0 且 grad f 、grad g 线性相关时有驻点,因此可以通过研究 F 的驻点研究 f 在 g=0 约束下的极值。 |
7
conge 2021-03-19 06:59:31 +08:00
各位,推荐个数学教材吧。
我要去回炉一下我的数学。 |
8
JensenQian 2021-03-19 07:14:16 +08:00 via Android |
9
conge 2021-03-19 08:48:18 +08:00
@JensenQian 谢谢。
|
10
futou 2021-03-19 09:52:04 +08:00
每天拉格朗日的路过。说大白话,能用拉格朗日的前提是你求解的满足约束的极值首先是存在的,然后是可求解的,也就是要求 f()在极值点处连续可微且与 g()相交。脱离这一大前提,要么无解要么不可解,再怎么思考也是空想。在这一大前提下参考#5 的说法,简单易懂。
另外建议学习拉格朗日的推广:KKT 条件。能查到 kkt 充分条件是 f() g()是凸函数,且要存在可行解。 另外,当你实际遇到一些不能用拉格朗日乘子法的时候,直接按步骤套进去,你会发现:1. 不能求导啊; 2. λ=0 啊; 3.λ等于任何值都成立啊 等等等等 |
11
huzhikuizainali OP @RingoTC 谢谢你的回复和配图。目前我所看到的拉格朗日乘数例题,都是求到原点距离的极值。你回复中配图的极值显然不是指到原点的距离。那么 f(x,y)表达式应该是怎么样的呢?
|